Simpson’s 3 8 Method C Code
I will share the Simpson’s 3 8 Method C Code. There are other methods that can calculate the integration more accurate but today I’ll share one of my class notes which can be helpful who is looking for an easy implementation of this method. The function that I use for this program is ex whose integration is same as itself. You can implement your custom function easily overriding f(double x) prototype. Program requires lower, upper bound of integration and the n ( part count ) as an input. You can get more accurate results when you give n is high enough. Because the method is applied each part independently. You can check out code of the program below. The method detailed information.
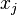 and numbers
and numbers  , the Lagrange polynomial is the polynomial of the least degree that at each point
, the Lagrange polynomial is the polynomial of the least degree that at each point