Simpson’s 3 8 Method C Code
I will share the Simpson’s 3 8 Method C Code. There are other methods that can calculate the integration more accurate but today I’ll share one of my class notes which can be helpful who is looking for an easy implementation of this method. The function that I use for this program is ex whose integration is same as itself. You can implement your custom function easily overriding f(double x) prototype. Program requires lower, upper bound of integration and the n ( part count ) as an input. You can get more accurate results when you give n is high enough. Because the method is applied each part independently. You can check out code of the program below. The method detailed information.
#include <stdio.h>
#include <stdlib.h>
#define _USE_MATH_DEFINES
#include <math.h>
double lower,upper;
int step;
double f(double x);
double simpson(double lower, double upper);
int main() {
printf("Please enter lower bound:");
scanf("%lf", &lower);
printf("Please enter upper bound:");
scanf("%lf", &upper);
printf("Please enter n:");
scanf("%d", &step);
double result=0;
double functionIncrement= (upper - lower)/ step;
for (int i = 0; i < step; i++)
{
double low = lower + i*functionIncrement;
double up = low + functionIncrement;
result += simpson(low, up);
printf("%lf %lf\n", low, up);
}
printf("Integration result is: %.10lf\n", result);
system("PAUSE");
return 0;
}
double f(double x){
return pow(M_E,x);
}
double simpson(double lower, double upper)//n=3 3/8 kuralı
{
double h = (upper - lower) / 3;
double mid = lower + h;
double mid2 = mid + h;
double res = (3 * h / 8)*(f(lower) + 3 * f(mid) + 3 * f(mid2) + f(upper)) - 3*pow(h,5)/80;
return res;
}
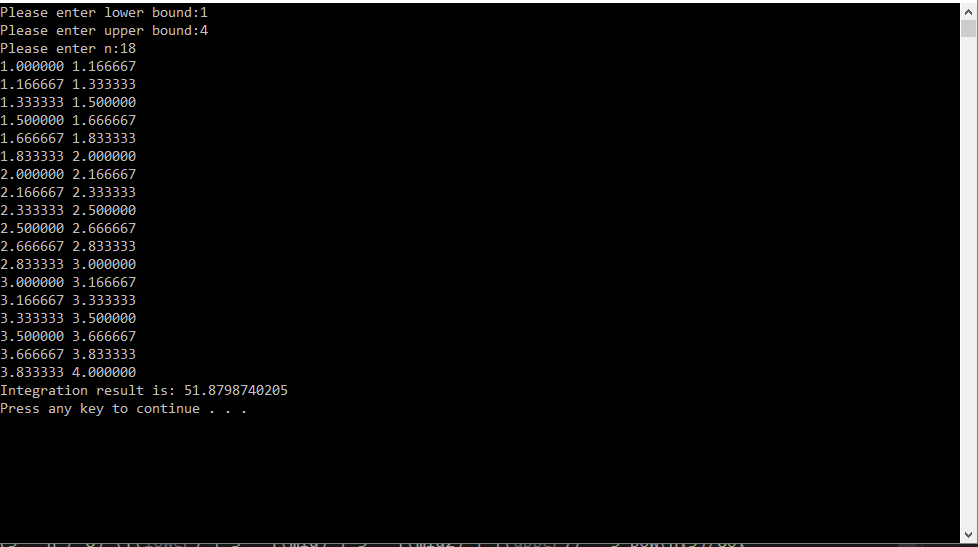
An example output when you run the program above.
Lower Bound : 1
Upper Bound : 4
n : 18
Result of the integration is : 51.8798740205
When you take the original function integration it gives us 51.8798682046852.
It shows that fault tolerance is in 4 decimal precision. When we give n : 100
The result becomes more accurate like 51.8798682108.
Leave a Reply