In numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points 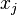 and numbers
and numbers  , the Lagrange polynomial is the polynomial of the least degree that at each point
, the Lagrange polynomial is the polynomial of the least degree that at each point 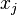 assumes the corresponding value
assumes the corresponding value  (i.e. the functions coincide at each point). The interpolating polynomial of the least degree is unique, however, and it is therefore more appropriate to speak of “the Lagrange form” of that unique polynomial rather than “the Lagrange interpolation polynomial”, since the same polynomial can be arrived at through multiple methods.
(i.e. the functions coincide at each point). The interpolating polynomial of the least degree is unique, however, and it is therefore more appropriate to speak of “the Lagrange form” of that unique polynomial rather than “the Lagrange interpolation polynomial”, since the same polynomial can be arrived at through multiple methods.
Given a set of k + 1 data points
where no two 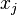 are the same, the Lagrange Interpolation form is a linear combination
are the same, the Lagrange Interpolation form is a linear combination
of Lagrange basis polynomials
where 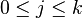 . Note how, given the initial assumption that no two
. Note how, given the initial assumption that no two 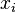 are the same,
are the same,  , so this expression is always well-defined. The reason pairs
, so this expression is always well-defined. The reason pairs 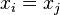 with
with  are not allowed is that no interpolation function
are not allowed is that no interpolation function  such that
such that  would exist; a function can only get one value for each argument
would exist; a function can only get one value for each argument 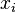 . On the other hand, if also
. On the other hand, if also  , then those two points would actually be one single point.
, then those two points would actually be one single point.
For all 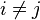 ,
, 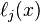 includes the term
includes the term 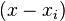 in the numerator, so the whole product will be zero at
in the numerator, so the whole product will be zero at  :
:
On the other hand,
In other words, all basis polynomials are zero at  , except
, except 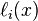 , for which it holds that
, for which it holds that  , because it lacks the
, because it lacks the 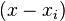 term.
term.
It follows that 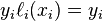 , so at each point
, so at each point 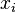 ,
, 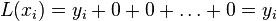 , showing that
, showing that  interpolates the function exactly. ( Definition Source : Wikipedia )
interpolates the function exactly. ( Definition Source : Wikipedia )
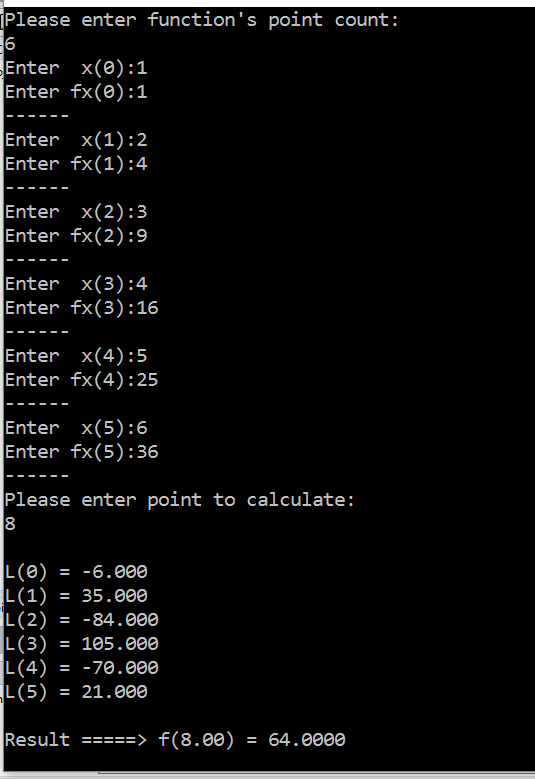
The Lagrange Interpolation C Code is written below.
#include <stdio.h>
#include <stdlib.h>
double Lagrange(int n, int k,double value);
double* fx;
double* x;
double Calculate(int n, double x);
void main() {
int size;
double question;
printf("Please enter function's point count:\n");
scanf("%d", &size);
fx = (double*)malloc(sizeof(double)*size);
x = (double*)malloc(sizeof(double)*size);
for (int i = 0; i < size; i++)
{
printf("Enter x(%d):", i);
scanf("%lf", &x[i]);
printf("Enter fx(%d):", i);
scanf("%lf", &fx[i]);
printf("------\n");
}
printf("Please enter point to calculate:\n");
scanf("%lf", &question);
printf("\n");
printf("Result =====> f(%4.2lf) = %5.4lf\n",question, Calculate(size, question));
printf("\n");
system("PAUSE");
}
double Lagrange(int n, int k, double val)
{
double result = 1;
for (int i = 0; i < n; i++)
{
if (i!=k)
result = result * (double)((val - x[i]) / (x[k] - x[i]));
}
return result;
}
double Calculate(int n,double x)
{
double intPolasyon = 0;
double *L = (double*)malloc(sizeof(double)*n);
double *F = (double*)malloc(sizeof(double)*n);
for (int i = 0; i < n; i++)
{
L[i] = Lagrange(n, i, x);
intPolasyon += fx[i] * L[i];
printf("L(%d) = %5.3lf\n", i, L[i]);
}
printf("\n");
return intPolasyon;
}
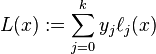
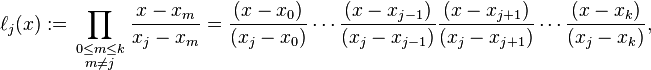
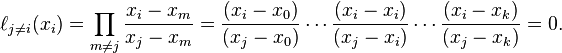

Leave a Reply